29: Removing the falseness (2)
Removing the falseness (2)
We now need to get rid of the falseness in the second cross section.
Let’s remind ourselves of a couple of constraints we put in place a while back:
- No bell may lie still for more than two blows.
- No bell can lie still in 5ths place unless the treble is in 6ths (for subtle musical considerations).
Given these two constraints, a little thought will show that there is only one way to eliminate the falseness in the second cross-section, when the Treble is dodging 3-4 up: we must introduce a set of ‘Oxford’ places (place notation x12x) in 1-2.
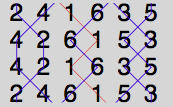
The same will apply when we get to the fifth cross section, when the treble is dodging 3-4 down:
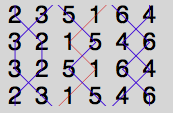
This is incredibly useful. It means that, in any method where the Treble follows a “Treble-bobbing’ path, we know exactly what must be going on for all the other bells when the Treble is dodging in 3-4:
- The bells in 5-6 must dodge with each other.
- The bell in 3-4 must dodge with the treble.
- One of the bells in 1-2 must make 2nds.
- The other bell in 1-2 must lead.
You can see all of this on the two diagrams above.
A couple of very useful things follow from this:
- If one of your bells has just dodged with the treble at the start of the lead, it MUST lead and then make seconds.
- If one of your bells arrives on the front as the treble is leaving, it MUST lead without dodging first.
The ‘Oxford’ places in 1-2 work just as well to remove all the falseness when the treble is in 5-6. If we do that, we will have removed all of the falseness. We have a true block of 24 changes. This block forms the first lead of the method which is the foundation of everything we’re going to do: Kent Treble Bob Minor.
The place notation is:
34-34.16-12-16-12-16-12-16-12-16.34-34
Notice that I’ve chosen to replace ‘x’ with ‘-‘. You will see either symbol used to represent all pairs crossing; ‘-‘ can look a bit clearer than ‘x’ in a long string of place notation.
The grid looks like this:
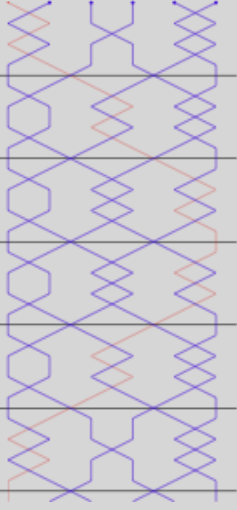
Take time to study, visualise and memorise the grid. It is absolutely key. Understand how it works and why it is designed in the way that it is. Understanding this fundamental grid will repay you richly in all your handbell ringing. If you understand the grid, you won’t have to memorise too many rules, since rules tend to follow from the design of the grid. For now, don’t worry about how to ring this grid, and don’t worry about what the individual bells (or pairs) are doing. Just remember that the Treble is represented by the red line and follows a treble-bobbing path. We’ll look at what all the other bells are doing when we work out how to set about ringing this stuff. For the moment, this is theory. The practical comes next!
Notice that the grid is symmetrical about the half lead. Putting it another way, the lower half of the grid is a reflection of the upper half. ALL commonly rung methods feature this half lead symmetry. Symmetry is a big help in change ringing. You only ever need to learn half a grid since the other half will always be a reflection.
The symbol ‘&’ is used to represent a reflection of a place notation, so the place notation above could be written more concisely as:
&34-34.16-12-16-12-16
Notice also that, in this grid, all the cross-sections are the same (place notations: -12-) apart from the first and last (place notations 34-34).
Notice too that the transitions from one cross-section to the next are all the same. One bell leads, and another bell lies (place notation 16). The other bells all move from one dodging position to the next. Since this happens at every backstroke in Plain Hunt, the bells are said to ‘hunt’ between cross sections. This constant hunting between cross-sections is a fundamental condition of a Treble Bob method. Not all methods do this. There are important classes of methods called ‘Delight’ and ‘Surprise’ where this does not happen. We’ll look at those later.
Exercise:
- On squared paper, write out the first 24 changes of Kent Minor and draw the lines through each bell.



